불 대수의 기본법칙
교환법칙
$A+B=B+A$
$A·B = B·A$
결합법칙
$A+(B+C) = (A+B)+C$
$(A·B)·C=A·(B·C)$
분배법칙
$A·(B+C)=A·B + A·C$
$A+(B·C) = (A+B)·(A+C)$
드모르간의 법칙
$\overline{(A+B)} = \overline{A} · \overline{B}$
$\overline{(A·B)} = \overline{A} + \overline{B}$
기본법칙
$A · 0 = 0$
$A · 1 = A$
$A + 0 = A$
$A + 1 = 1$
$A + \overline{A} = 1$
$A + A = A$
$A · A = A$
기본정리
$A + A·\overline{B} = A$
$A+\overline{A}B = (A+\overline{A})·(A+B) = 1·(A + B) = A + B$
$\overline{A} B + \overline{B} =(\overline{A} + \overline{B})·(B + \overline{B}) = \overline{A} +\overline{B} =\overline{A·B}$
위 식은 분배법칙으로 유도된다.
카르노맵
맵을 그리기 전에 카르노맵이 어떻케 나왔는지 생각해보자.
다음과 같은 대수식이 있다. 이것을 간단히 하면,
$F=\overline{A} B + A \overline{B} + AB$

즉, 카르노맵은 공통인수가 포함되도록 묶고(2,4,8,16...,) 묶인 부분의 공통인수는 남기고 1이 되는 요소(예, $A + \overline{A}$)는 버리는 형태를 가진다. 많이 묶자. 상하좌우 벽을 통과한다. 단, 대각으로는 묶지 못한다.

3변수는

4변수는
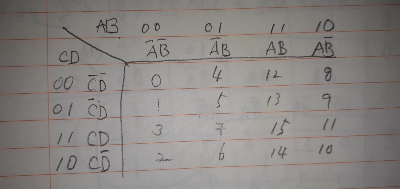
과 같은 형태를 가진다. 3변수와 4변수 내에 있는 숫자는 ABCD의 2진 숫자를 10진 숫자로 나타낸 값이다.
$F(A,B,C,D)=\Sigma(4,5,12,13,15,16) $로 표시되는 카르노맵은 아래와 같으며 간략화된 부울대수값도 나타내었다.

그리고 마지막으로 4 귀퉁이가 모두 1인 카르노맵은 4 귀퉁이를 하나로 모아 묶을 수 있다.

'전기, 전자' 카테고리의 다른 글
| 접점(a, b, c 접점) (0) | 2020.09.18 |
|---|---|
| 계전기(Relay) (0) | 2020.09.18 |
| 다이오드와 트랜지스터 극성 찾기 (0) | 2020.04.23 |
| 커패시터 읽는 법 (0) | 2020.04.23 |
| 저항 읽는 법 (0) | 2020.01.24 |


