<초기삼각비>

$sin \theta = c/b$
$cos \theta = a/c$
$tan \theta = b/a$
산을 타고 올라가면 절벽에서 떨어지는 거리와의 비가 SIN이라고 정의했다.
COSINE은 COmpliment의 'CO'를 따왔다. ($90˚-\theta$). 산 정상에서 산을 타고 내려온 거리와 떨어진 위치와 수평거리의 비가 된다.
tan은 기울기로 정의된다.
<단위 원에 내접하는 삼각형의 삼각비>

sin은 y값에 대응된다. cos은 x 값에 대응된다. tan는 외접하는 직선의 길이가 된다.
우측 접선까지의 거리는 1, 접선과 $\theta$ 각도를 이루고 탈출하는 선이 만나는 곳의 각도는 $90˚-\theta$가 된다.
작은 삼각형과 큰 삼각형은 합동이므로
x:y= 1:높이
높이 = y/x
가 되고 이것이 tan가 된다. tan은 tangible(명백한이란 뜻이나 손에 잡힌다라는 어원이 있다. 손에 잡히니 똥인지 된장인지 알 수 있겠지... entangle 마법도 같은 어원에서 나왔다.)
<탄젠트비>
$tan \theta = \dfrac {sin \theta} {cos \theta}$
<삼각비의 역수>
$cosec \theta = \frac{1}{sin \theta}$
$sec \theta = \frac{1}{cos \theta}$
$cot \theta = \frac{1}{tan \theta}$
<특정각도 외우기 팁>
$sin 0˚ = 0 = cos 90˚$
$sin 30˚ = \frac {1} {2} = cos 60˚$
$sin 45˚ = \frac {\sqrt{2}} {2} = cos 45˚$
$sin 60˚ = \frac {\sqrt {3}} {2} =cos30˚$
$sin 90˚ = \frac {\sqrt {4}} {2} = 1 = cos 0˚$
$tan 0˚ = 0$
$tan 30˚ = \frac{1}{\sqrt{3}}$
$tan 45˚ = \frac{\sqrt{3}}{\sqrt{3}} =1$
$tan 60˚ = \frac{\sqrt{3} \sqrt{3}}{\sqrt{3}}= \sqrt{3}$
$tan 90˚ = \infty$
<역함수>
$\theta = Sin^{-1} (c/b)$
$\theta = Cos^{-1} (a/c)$
$\theta = Tan^{-1} (b/a)$
<제곱 공식>

위 그림은 다음과 같이 그린다. 먼저 일반 삼각형 3개를 바람개비처럼 만든다. (핵 위험 표지와 비슷하기도 하다) 가운데 1을 기입한다. sin을 시작으로 sin의 compliment인 cos를 우측에 그린다. sin과 cos을 그렀으니 아래의 왼쪽 모서리에 tan을 기입한다. 그리고 나서 가운데 접히는 1을 지나서 대칭이 되는곳에 역수가 되는 값을 적는다.
예) tan는 1을 지나면 cot, cos는 1을 지나면 sec, sin은 1을 지나면 cosec.
미분일 경우에는 좌에서 우면 부호변동 없고, 우에서 좌면 부호변동 있다.
적분일 경우에는 부호변동이 반대이다.
(각 삼각형의 상변 꼭지점의 제곱은 하단 꼭지점의 제곱과 같다)
$sin^{2} \theta + cos^{2} \theta = 1$
$1+tan^{2} \theta = sec^{2} \theta$
$1+cot^{2} \theta = cosec ^{2} \theta$
<미분 공식>
최상단은 부호고려와 변신
$\frac{\mathrm{d} }{\mathrm{d} x}sin \, x = cos \, x$
$\frac{\mathrm{d} }{\mathrm{d} x}cos \, x = -sin \, x$
중간층은 부호고려와 이웃의 제곱
$\frac{\mathrm{d} }{\mathrm{d} x}tan \, x = sec^2 \, x$
$\frac{\mathrm{d} }{\mathrm{d} x}cot \, x = -cosec^2 \, x$
최하단은 부호고려와 자기와 이웃과의 곱
$\frac{\mathrm{d} }{\mathrm{d} x}sec \, x = sec \, x tan \, x$
$\frac{\mathrm{d} }{\mathrm{d} x}cosec \, x = -cosec \, x cot \, x$
<적분 공식>(상수 생략)
$\int sin \, x = -cos \, x$
$\int cos \, x = sin \, x$
미분과 적분/삼각함수 적분 - 위키책
삼각함수의 적분은 아래와 같다. ∫ cos x d x = sin x + C {\displaystyle \int \cos {x}\,dx=\sin {x}+C} ∫ sin x d x = − cos x + C {\displaystyle \int \sin {x}\,dx=-\cos {x}+C} ∫ tan x d x = − ln | cos x | + C {\displaystyle \int \tan {x}\,dx=-\ln {\left|\cos
ko.wikibooks.org
All-Sin-Tan-Cos(얼싸안꼬) 공식 (I)
$sin (-\theta) = - sin \theta$
$cos (-\theta) = cos \theta$
$tan (-\theta) = -tan \theta$
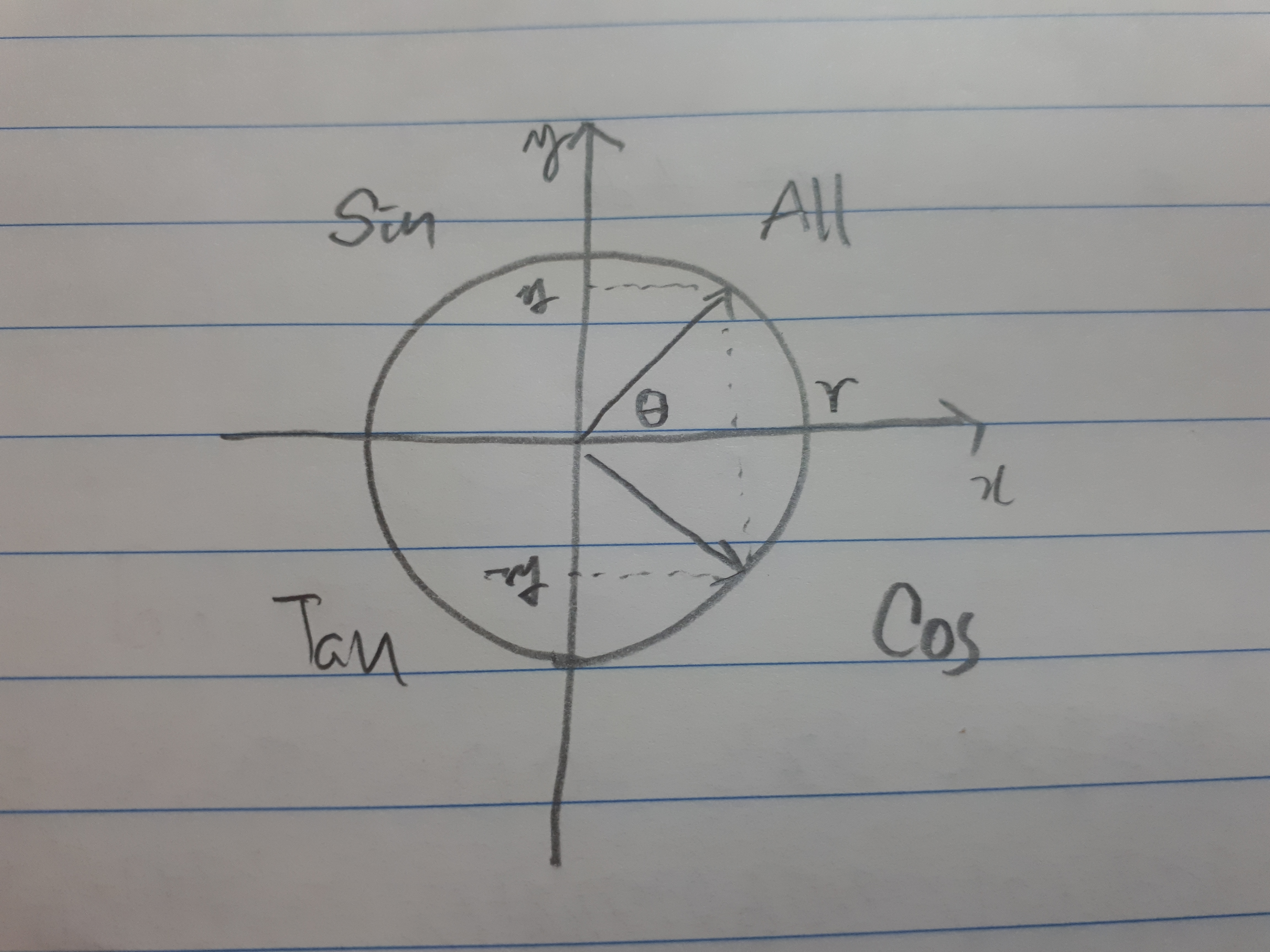
$\theta$가 $-\theta$라는 것은 1사분면에서 4사분면으로 이동한다는 것이다. 그러면 이 이동은 x축에 대칭관계이며 y값이 음수로 변한다. 단, 코사인 값은 y값을 이용하지 않으므로 그림과 같이 4사분면에서는 코사인 내부의 마이너스 값이 밖으로 나올 필요가 없다.
All-Sin-Tan-Cos(얼싸안꼬) 공식 (II)
$n\pi/2$에서 n이 홀수이거나 짝수일 경우:
n이 홀수 : sin -> cos, cos->sin, tan -> cot로 변경한다.
n이 짤수 : sin -> sin, cos->cos, tan->tan
$sin(90 + 30) = cos30$
$sin(90 - 30) = cos(-30)=cos30$
$sin(180 + 30) = -sin(30)$
$sin(180 - 30) = -sin(-30)=sin30$
$cos(90+30)=-sin(30)$
$cos(90-30)= -sin(-30) = sin30$
$cos(180+30)=-cos30$
$cos(180-30)=-cos(-30)=-cos30$
<덧셈공식>
윗 얼싸안꼬 공식은 아래 덧셈공식(회전공식)의 일부임을 알 수 있다.
$sin(\alpha \pm \beta) = sin \, \alpha cos \, \beta \pm cos \, \alpha sin \, \beta$
$cos(\alpha \pm \beta) = cos \, \alpha cos \, \beta \mp sin \, \alpha sin \, \beta$
$tan(\alpha \pm \beta) = \dfrac{tan \, \alpha \pm tan \, \beta}{1 \mp tan \, \alpha tan \, \beta}$
삼각함수의 덧셈공식은 절대로 잊어버리면 안된다. 자동제어에서 다시 만나게 될 것이다.
신데렐라가 신코픈 꽃신을 신고 있는데
마녀는 고구마사소하네. (사과가 아닌가?)
일마탄탄 분의 탄프탄(백마탄탄분의 탄도탄 맞고 사망)
덧셈공식은 오일러 공식으로 증명하는게 가장 쉽다.
$e^{j(\alpha + \beta)} = cos (\alpha + \beta) + j sin (\alpha+\beta)$ ------- (1)
$e^{j(\alpha + \beta)} = e^{j \alpha} \cdot e^{j \beta} = (cos \alpha + jsin \alpha)(cos \beta + jsin \beta)$ ------- (2)
식(2)를 풀어서 실수부와 허수부를 나누어서 정리하면
$cos \alpha cos \beta - sin \alpha sin \beta + j(sin \alpha cos \beta + cos \alpha sin \beta)$ ------- (3)
가 나온다.
식(3)을 식(1)과 비교하면, 덧셈공식이 증명된다.
<회전공식>
덧셈공식을 회전공식이라고도 하는데 행렬로 푸는 방법도 있다.
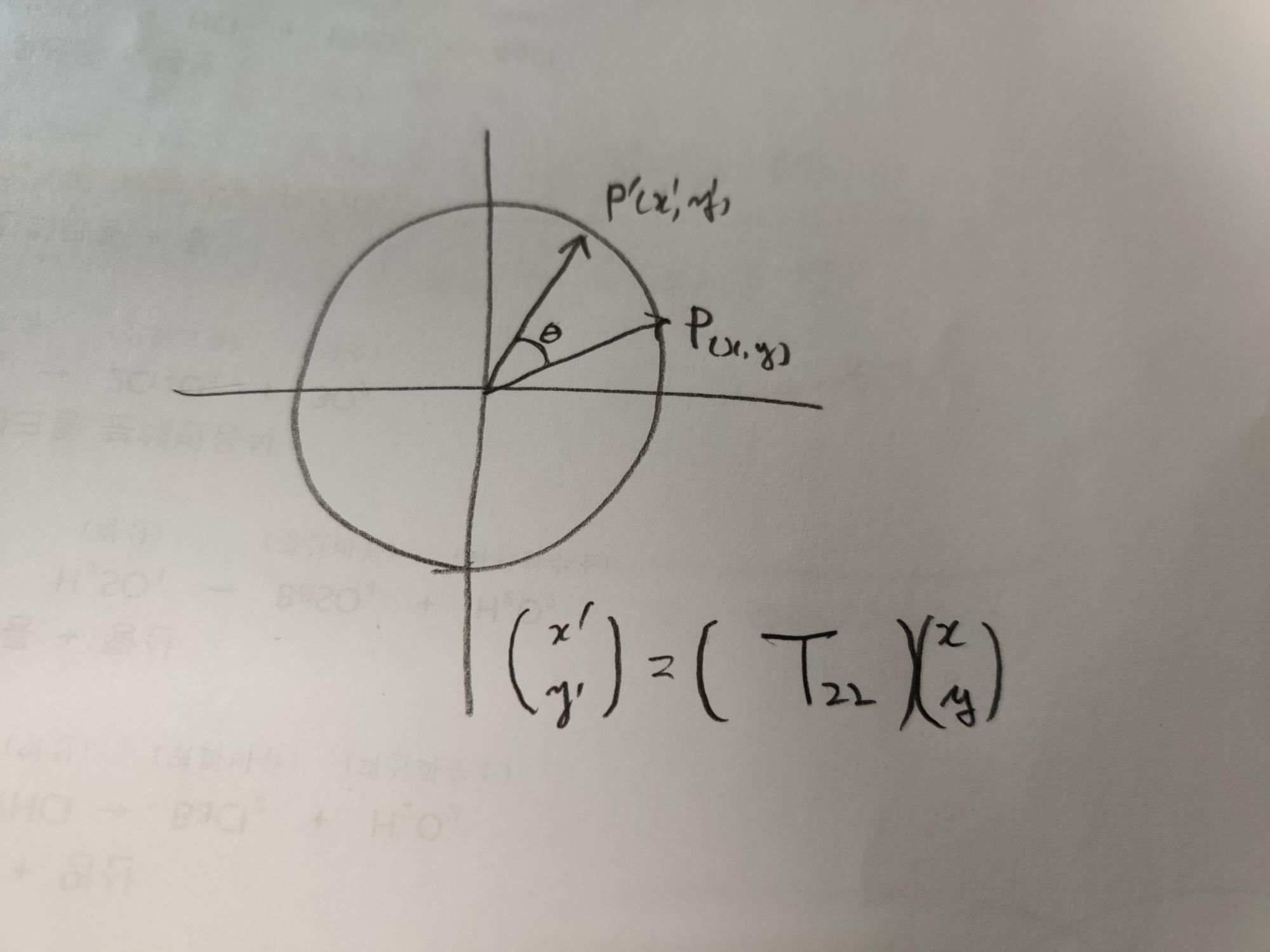
위 그림에서 매트릭스 $T_{22}$는
$T_{22}=\begin{pmatrix} cos \theta & -sin \theta \\ sin \theta & cos \theta \end{pmatrix}$
로 나타난다.
회전변환
1차 변환 가운데 하나인 회전변환을 탐구해 보자. 삼각함수의 덧셈정리를 알고 있다면 아주 간단하게 증명할 수 있다. 여기서는 그냥 그림으로 설명해 보려고 한다. 그림에서 점 $P$를 원점을 중심으로 $\theta$..
suhak.tistory.com
'수학' 카테고리의 다른 글
| 수학에서 라디안(Radian)이란? (0) | 2024.06.12 |
|---|---|
| 평행사변형의 대각선 길이 (0) | 2023.06.27 |
| 곱셈과 미적분 이해하기 (0) | 2022.12.02 |
| 원과 구 (0) | 2020.03.12 |
| 주파수와 주기 (0) | 2020.01.28 |


