등차수열, 급수(삼각수), 멱급수, 구분구적법, 푸리에변환
등차수열
아래 수열은 등차수열이다.

앞 수에 항상 1을 더한 값이 다음에 나타나기 때문이다.
일반적인 표기법도 알아보자.
윗 등차수열을 n번째 항까지 일반화해서 나열하면 아래와 같이 쓸 수 있다.

여기서 초기항 a1의 값을 a라 하고, 등차를 d라고 하면,
윗 수열은 아래와 같이 나타난다.

그리고 윗 수열의 n번째 항은 아래와 같이 쓰게되며 이는 일반적인 수열의 n번째 항을 나타낸다라고 한다.

또는

이다.
급수(삼각수)
그리고 이러한 공차수열의 합(급수)는 아래의 시그마 기호를 사용해서 표시할 수 있으며 또한 그 공식은 아래와 같다. 이것은 "평균값X갯수"라는 의미이다.

바로 이 급수가 "삼각수"이다. "삼각수"는 초기항이 1이고 등차가 1인 수열의 합(급수)를 의미한다. "삼각수"라 이름 붙여진 이유는 삼각형 형태를 만들어 가는 수이기 때문이다. 즉, 급수가 삼각형을 만들어 낸다.

멱급수
그러면 이러한 "삼각수"의 각 항에 제곱을 한 수열을 생각해보자. 일반 항의 점화식은 아래와 같이 쓸 수 있다.

그리고 이러한 수열의 합은 아래의 급수로 쓸 수 있다.

이것은 ∑이라는 기호를 가져와서 써보자.

바로 위의 수식과 같이 각 항에 제곱한 형태를 가지는 급수를 멱급수라고 한다. 영어의 power에서 가져온 한자어인데 각 항에 1이 아닌 지수가 붙은 형태이면 멱급수로 보면된다.
수식 (2)의 해를 찾아보자.
이러한 해를 찾는 요령은 각 항의 관계에 대한 일반식을 세우는 것이다. 그리고 하나의 차수를 더 키워서 생각하는 것이다.
즉, 어느 하나의 숫자(x)에 1 더한값의 세제곱값은 (x+1)3이며 그 숫자와의 차이는 아랫식으로 구할 것이다. 단 그 차이는 아직 미정이다.

이것을 풀어 써보자.

수식 (3)에 1부터 n까지 대입해보자.

좌변과 우변을 각각 모두 더해주면,

아래의 항등식이 성립한다.

윗 식을 ∑을 이용해서 묶으면,

3∑nk=1k2 항을 좌변으로 하고 정리하면,

여기서

이므로

이것을 풀면,

즉, 수식 (4)가 각 항의 제곱인 멱급수의 합 공식이다.
여기서 잠깐 윗 유도방법은 수식 (1)에도 적용되는가?
당연히 적용된다. 앞선 유도에서 보듯이 한 차수를 늘려서 an+12과 an2의 차잇값을 구하는 형태를 만들면, 원 차수의 형태가 나타나기 때문에 아래의 항등식 형태를 만들고 윗 풀이과정을 반복하면 된다.

자 그럼 아랫 수식도 풀 수 있는가?

수식 (4)를 유도한 방법을 그대로 적용해서 풀기위해서 아래와 같은 항등식을 세워서 시작하면 된다.

1부터 n까지 대입한 후 양변을 각각 더한 후, x3, x2 및 x 항을 모두 알기 때문에 쉽게 아래의 수식을 얻을 수 있다.
![\sum_{k=1}^{n}k^3 = \Big[\frac{n(n+1)}{2}\Big]^2 --- (6)](http://t1.daumcdn.net/tistory_admin/static/images/xBoxReplace_250.png)
구분구적법
구분구적법 대신 시그마와 리미트가 함께 있으면, 적분 구간이 생성되므로 정적분으로 소제를 붙이려다가 구분구적법의 원리가 더 중요하므로 소제목을 위와 같이 두었다. "시그마와 극한이 합치면 정적분이 된다"는 내용도 중요하다. 아랫 수식을 보자.

윗 수식을 풀 수 있는가?
일견 윗 수식의 답은 0으로 보인다. 왜냐하면 분자와 분모를 n4으로 나누면 분모는 1이 되고, 분자는 1/n이 되어서 n이 무한대로 증가하면 0이 되는 것처럼 보이기 때문이다. 그러나 틀렸다.
어떻케 아냐고? 우리는 수식 (6)의 해가 4차항을 가지고 있음을 이미 유도했기 때문이다. 수식 (6)을 대입하면 아래와 같다.
![\lim_{n \to \infty} \frac{1}{n^4} \left[\frac{(n(n+1)}{2}\right]^2 = \frac{1}{4} ---(8)](http://t1.daumcdn.net/tistory_admin/static/images/xBoxReplace_250.png)
먼저, 구분구적법을 이용한 정적분의 형태를 보면 아래와 같다.

윗 수식을 이용하기 위해서 수식 (7)을 아랫처럼 변형해보자.
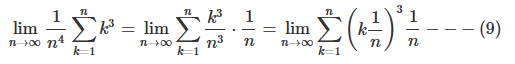
여기서 n이 무한대로 증가하므로 1/n는 Δx로 놓을 수 있다. 여기서 정적분의 시작항이 0이므로 xk=kΔx가 된다.
그러므로 수식 (9)는 f(x)=x3이므로 아래의 정적분과 같으며 그 해는 아래와 같다.
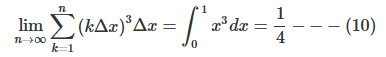
정적분 구간이 0부터 1이 된 이유는, 1⋅Δx=0이고 n⋅Δx=1이기 때문이다.
푸리에급수
푸리에 급수는 아랫 식으로 정의된다.
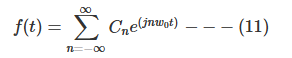
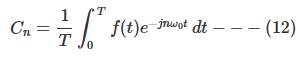
수식 (11)과 (12)는 주기함수 f(t)가 특정주파수의 합이라는 것을 잘 표현하고 있다. 푸리에급수에 대해서 더 알아보고 싶다면 아랫 포스팅을 참고하면 된다.
등비수열, 등비수열의 합, 테일러급수, 푸리에급수
등비수열아래 수열은 등비수열이다.1,2,4,8...앞 수에 항상 등비인 2를 곱한 것이 다음에 나타나기 때문이다. (다음 수가 이전 수에 2도 곱하고 3도 곱해서 나타나면 등비수열이라고 하지 않는
fotc.tistory.com
푸리에급수는 다시 말하지만, 주기함수(f(t))에 대해서만 성립한다.
그렇다면, 주기함수가 아닌 ˙f(t)의 푸리에급수(주파수특성)를 구할 수 있을까? 여기서 ˙f는 비주기함수를 강조하기 위한 표현이다.) 답은 "있다"이다. 어떻케? 비주기함수를 주기함수처럼 보이게 만들어주면 된다.
먼저 아랫 그림과 같이 비주기함수인 펄스함수 ˙f(t)가 있으면, 그 그래프는 아래와 같다.
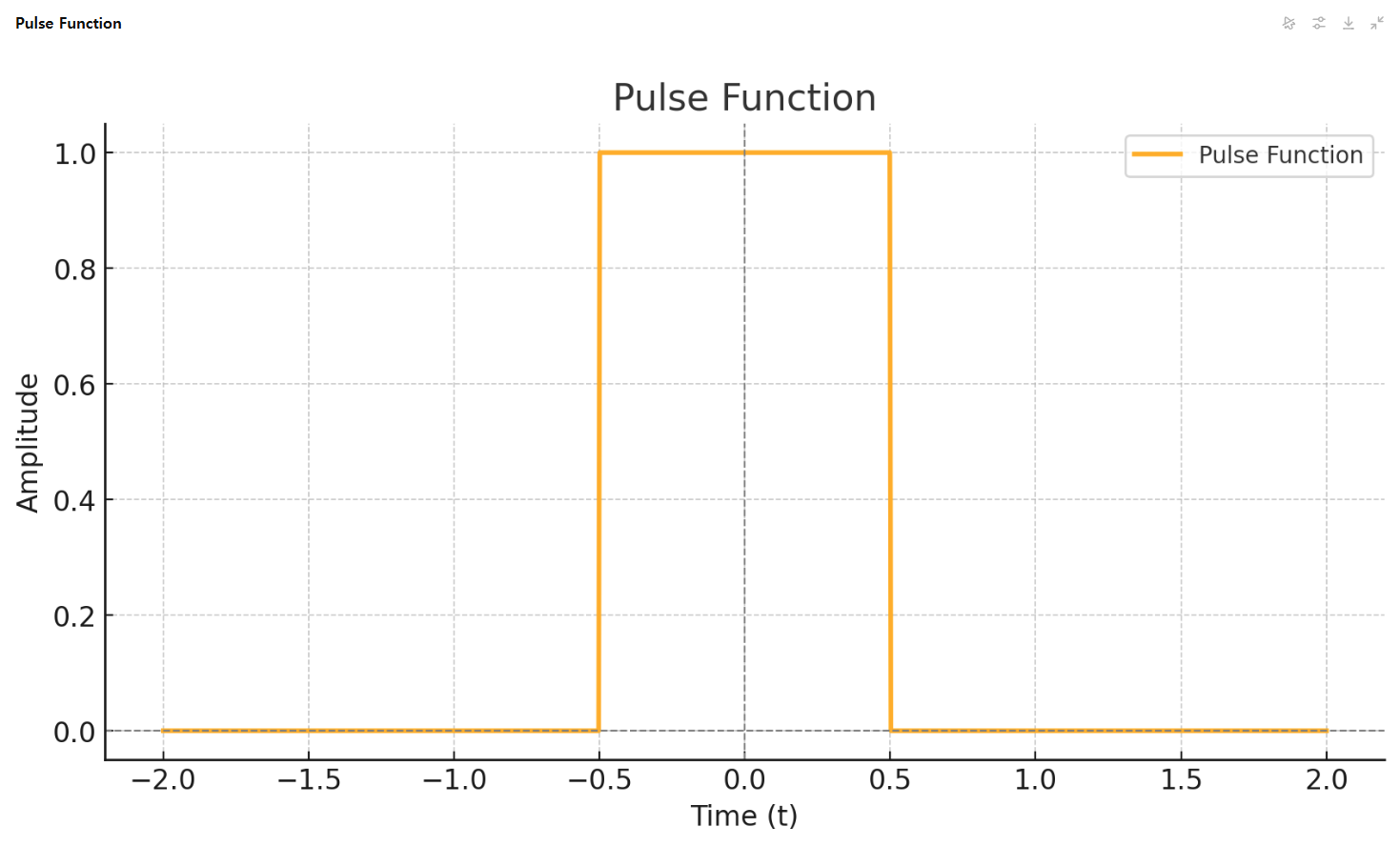
윗 그림은 주기 함수가 아닌 펄스함수 한 개를 그린 그래프이다. 이것은 주기 함수가 아니다. 위에서 주기를 무한대로 늘리면 된다고 했는데 정말 그런지 조금씩 주기를 늘려가면서 보도록 하자.
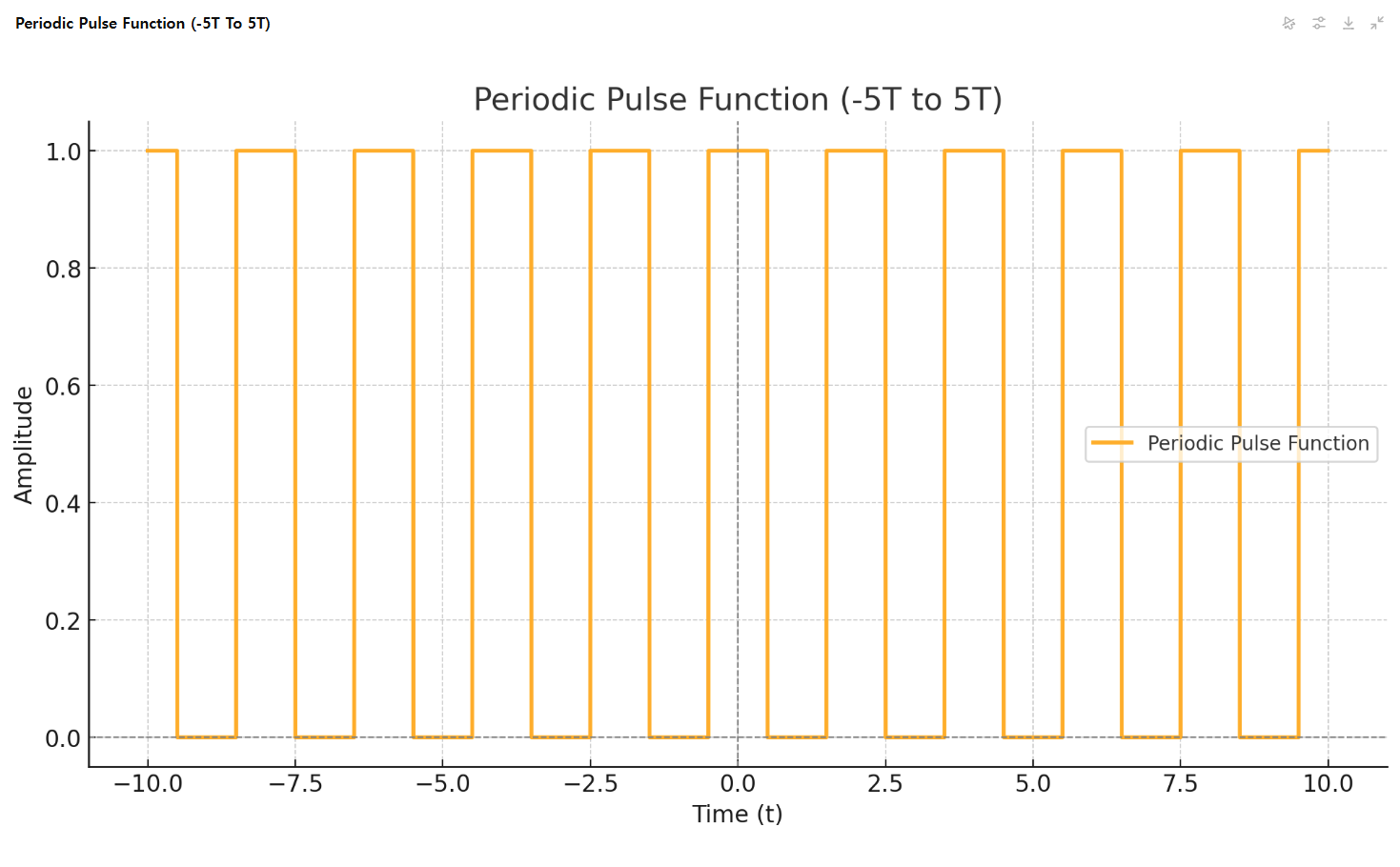
아래는 윗 펄스함수가 주기(T)를 가지는 주기함수(f(t))라고 생각했을 때의 그래프이다.
그리고 그림 4와 5는 주기 T를 2배, 4배해서 그렸다.
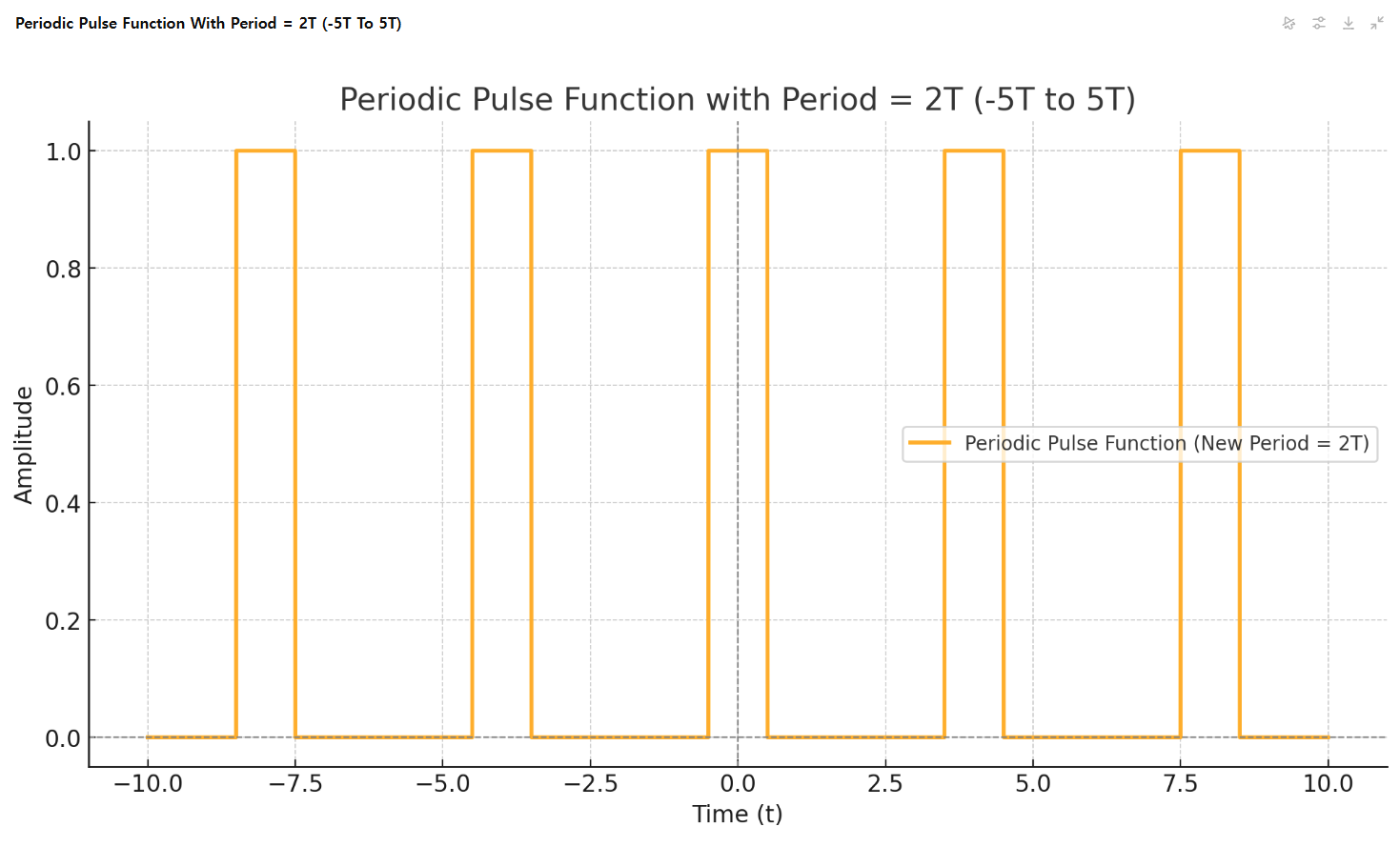
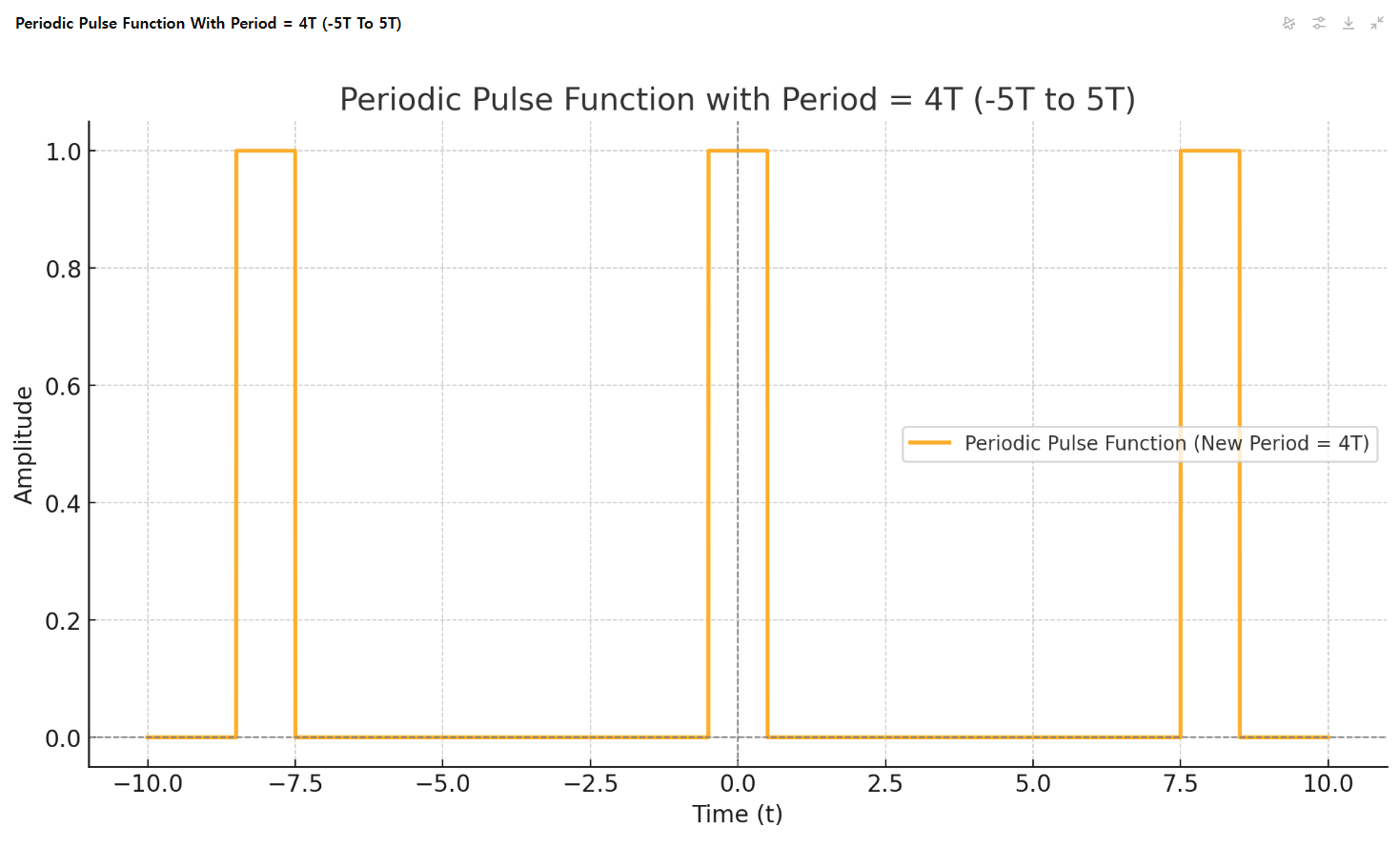
그렇다면 주기를 무한대로 늘리면 어떻케 될까? 즉, 주기가 무한대인 주기함수이면 펄스함수는 t=0 근처에서만 값(=1)을 가지고 그 이외에서는 아직 주기가 돌아 오지 않았으므로 값(=0)을 가지는 주기펄스함수(f(t))가 될 것 같다. 아래의 그래프를 확인해보자.
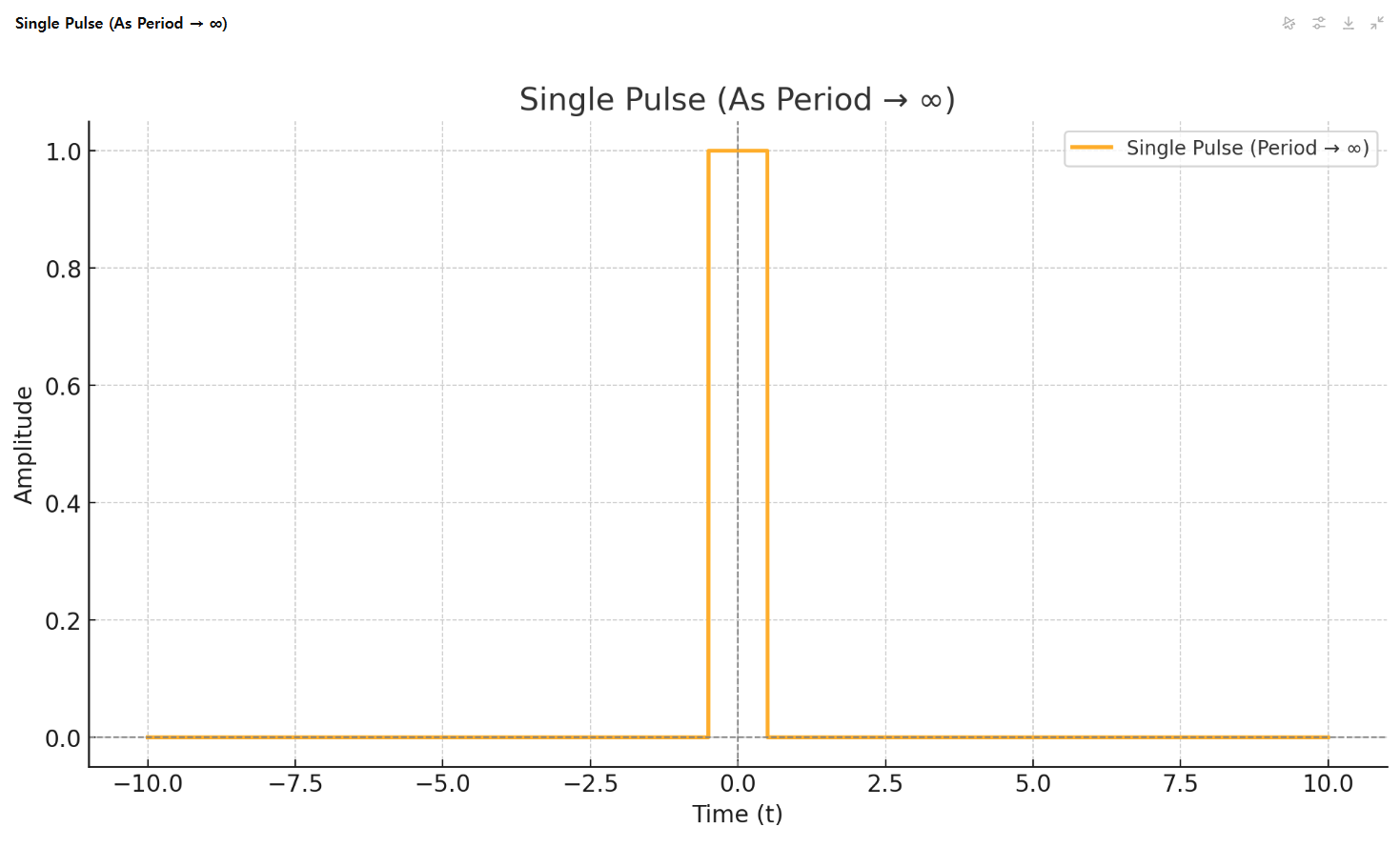
그림 2와 그림 6을 비교해 보니 비주기 펄스함수(˙f(t))와 주기 펄스함수(f(t))는 동치이다. -0.5t부터 0.5t까지만 1이고 그 이외의 영역에서는 모두 0이기 때문이다.
즉, 비주기 함수에 푸리에급수를 적용하기 위해서는 함수의 주기(T)를 ∞로 늘려주면 된다는 것을 알 수 있다.
![\begin{equation*}f(t)=\lim_{T \to \infty}\sum_{n=-\infty}^{\infty}\Big[\frac{1}{T}\int_{0}^{T}\dot f(t)e^{{(-jnw_0t)}}dt\Big]e^{(jnw_0t)}--- (13)\end{equation*}](https://blog.kakaocdn.net/dn/bVPxrU/btsLe3ru7pa/x0mEV13uC8FyPASh8NovZK/img.png)
그런데, 수식 (13)은 틀렸다. 왜냐하면 ˙f(t)가 비주기 함수이므로 적분구간을 이 함수를 품을 수 있는 구간으로 설정해야 된다. (주기함수에서는 적분 구간은 중요하지 않고 이 적분 구간이 주기 값이면 된다.)
그럼 −T에서 T로 놓으면 될까? 안된다. 그러면 맨 앞의 주기를 2T로 바꾸어 주어야 되며 이에 따라서 구분구적법을 이용해서 리미트와 시그마를 정적분으로 변환할 때 번거러워진다. 아래처럼 정적분 구간을 변경해주자.
![f(t)=\lim_{T \to \infty}\sum_{n=-\infty}^{\infty}\Big[\frac{1}{T}\int_{-T/2}^{T/2}\dot f(t)e^{{(-jnw_0t)}}dt\Big]e^{(jnw_0t)}--- (14)](https://blog.kakaocdn.net/dn/GMWrU/btsLfnJ73rI/vYVF056Aiy4vtZ9LTizO81/img.png)
이제 위에서 배운 구분구적법을 이용해서 리미트와 시그마를 없애주겠다.
먼저 주기의 역수인 (1/T)를 주파수로 변경한 후 각주파수항을 가지도록 변경해준다.
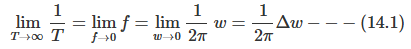
이 값을 리미트와 시그마 앞으로 옮겨 주어서 리미트와 시그마를 탈출한 것 처럼 쓴다.
![f(t)=\frac{1}{2 \pi}\Delta w\lim_{T \to \infty}\sum_{n=-\infty}^{\infty}\Big[\int_{-T/2}^{T/2}\dot f(t)e^{{(-jnw_0t)}}dt\Big]e^{(jnw_0t)}--- (14.2)](https://blog.kakaocdn.net/dn/cyu5KY/btsLhqSkQio/k84wgccP1Ou9JiZHL5ZPbk/img.png)
대괄호 부분에 리미트를 먼저 적용해보자.
![\lim_{T \to \infty}\Big[\int_{-T/2}^{T/2}\dot f(t)e^{{(-jnw_0t)}}dt\Big] =\int_{-\infty}^{\infty}f(t)e^{{(-jwt)}}dt --- (14.3)](https://blog.kakaocdn.net/dn/VTuYJ/btsLfx0e6ev/ZShLkQYVvt4tcsif3b2mak/img.png)
이것은 비주기함수 ˙f(t)에 주파수성분을 곱한 후 전체영역에 걸쳐서 정적분한 결과이다. 이를 X(w)라 놓으면 아래의 관계식이 도출된다. 바로 이 함수($X(f))가 푸리에 변환된 함수이며 다음과 같이 정의된다.
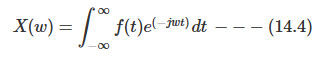
종종 "어떤 함수의 푸리에변환을 구하시오"라고 말할 때 윗 수식처럼 만들어 주는것이 푸리에변환 또는 푸리에 트랜스폼(FT:Fourier Transform)이다. 수식 (14.4)를 수식 (14.2)에 넣으면 아래의 수식이 유도된다.
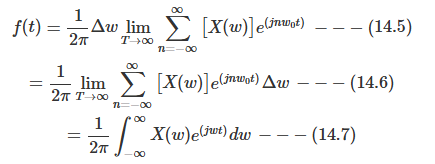
여기서 각주파수 대신 주파수에 대해서 표현하면 아래와 같이 된다.
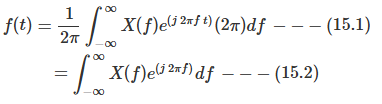
수식 (14.4)의 각주파수를 주파수로 표시했을 때 푸리에변환은 아래와 같다.
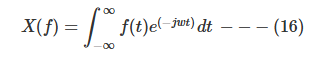
즉, 푸리에변환은 원 비주기 함수 ˙f(t)를 주기함수 f(t)로 보고(T→∞)를 취했기 때문) 여기에 e−j2πft를 곱한 후 시간영역에서 음의 무한대부터 양의 무한대까지 정적분하는 것이다. 또한, 역푸리에르변환은 푸리에변환 함수 X(f)에 ej2πft를 곱한 후 주파수영역에서 음의 무한대부터 양의 무한대까지 정적분하면 된다.
'수학' 카테고리의 다른 글
| 등비수열, 등비수열의 합, 테일러급수, 푸리에급수 (1) | 2024.12.05 |
|---|---|
| 수학에서 라디안(Radian)이란? (0) | 2024.06.12 |
| 평행사변형의 대각선 길이 (0) | 2023.06.27 |
| 곱셈과 미적분 이해하기 (0) | 2022.12.02 |
| 원과 구 (0) | 2020.03.12 |



